计算方法:插值与数值逼近

多项式插值

多项式插值要做的就是,找一个多项式 来近似任意函数 。

为了让插值尽量精确，我们让 经过所有的 （插值节点）。这样就得到：

显然这个方程组的解是唯一的，即：多项式插值具有唯一性。Lagrange 插值、Newton 插值等只是得到这个方程组的解的不同方式，最终得到的结果是一样的。

Lagrange 插值

计算

其中

事实上， 的本质就是 类似布尔函数.

被插函数可以表示为 ，其中 即为误差（又叫「插值余项」）。

误差 / 余项

其中 。

容易得到误差上限 。事实上，因为多项式插值是唯一的，所有多项式插值的误差和上限都是这个东西。

Newton 插值

计算

将 次插值多项式写成如下的形式：

其中：

为了便于表示，引入差商的定义。

差商

从上到下依次称「一阶差商」「二阶差商」……「 阶差商」。可以证明，。

用差商表示的 Newton 插值多项式：

误差 / 余项

由于多项式插值的唯一性，这个式子的值和 Lagrange 插值的余项是相等的，由此可以得到差商和导数的关系：

其中 。

差分与等距节点的插值

差分

• 阶向前差分：；
• 0 阶向前差分：；
• 阶向后差分：；
• 0 阶向后差分：；
• 阶中心差分：；
• 0 阶中心差分：。

向前差分与差商的关系：。

Newton 向前插值公式

用差分代替 Newton 插值公式中的差商：

用 代替 ：

（组合数公式：。广义的组合数中 可以是负数、小数）

Newton 向后插值公式

起始点选 ，使用向后的差分，可以推出下面的 Newton 向后插值公式。

函数的最佳平方逼近

问题描述

先来看连续情况.给定函数 是上n+1个线性无关函数，找一个 ，使得

即左侧的积分式取得最小值。式中 是权函数，满足：

• ；
• 存在，；
• 对任何非负函数 ，若 ，则 。

求解

记 。

记 。令 ，有

记 为 。令 的所有偏导为零，得到下面的线性方程组：

求解这个方程组，即可得到最佳平方逼近时的系数。

误差

记 ，记 为「平方误差」，记它的平方根 为「均方误差」。

正交函数与正交多项式

对 ，记 ，若 ，称 、 在 上带权 正交，记作 。

如果函数序列 在 上两两带权 正交，称 为 上带权 的正交函数族。

例如： 是在 上带权 的正交函数族，因为

如果 为首项系数非零的 次多项式，称 为正交多项式族。

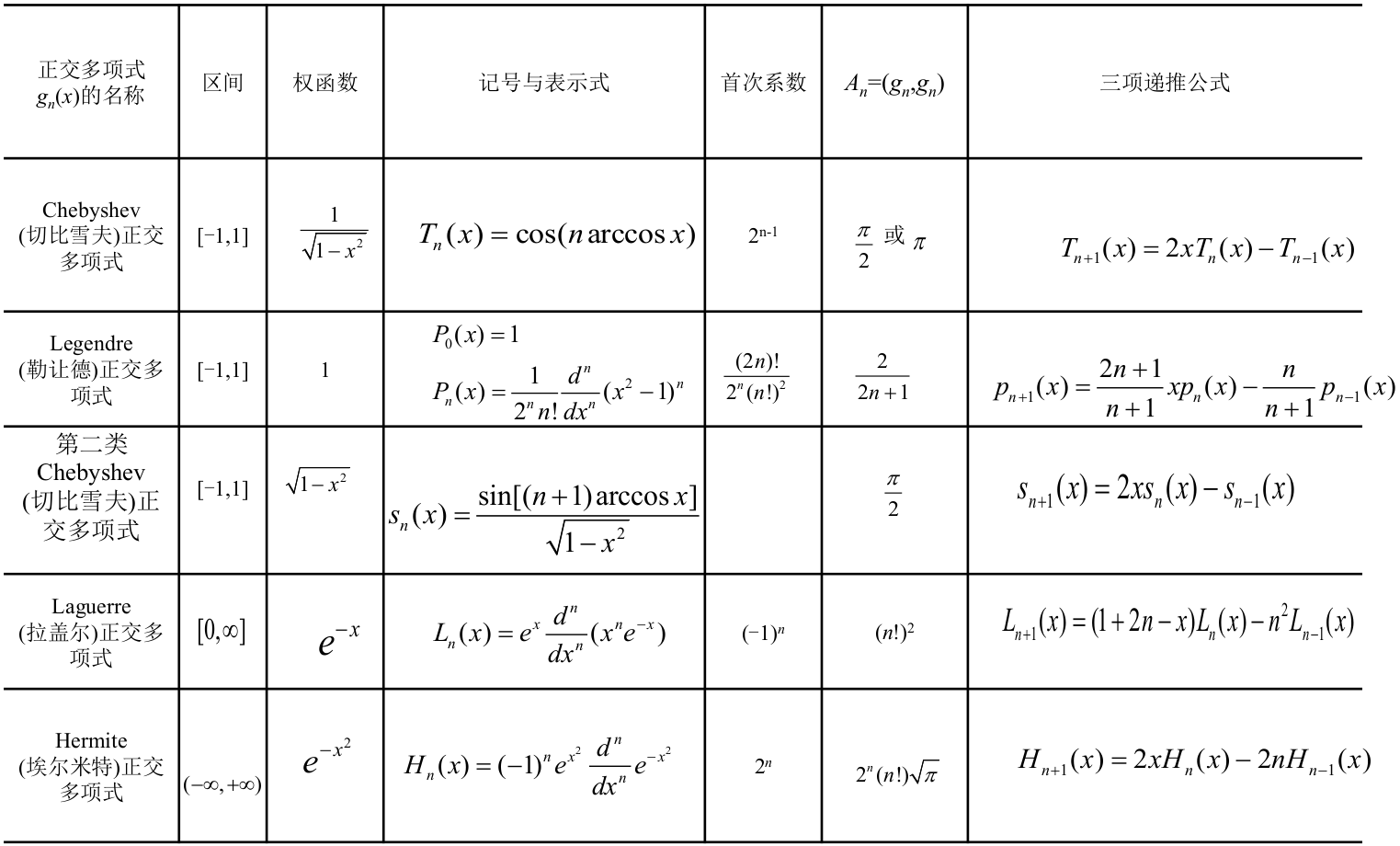
使用正交多项式族作为 进行最佳平方逼近，这样得到的左侧矩阵是对角阵。

曲线拟合（最小二乘法）

曲线拟合即是离散情况的最佳平方逼近问题。给定已知 个数据点的离散函数 ，找一个 ，使得

定义离散情况的内积

使用与前文相同的解法，可以解出系数 。

同样可以定义离散情况下的平方误差

以及均方误差

特别注意，在曲线拟合这里的「均方误差」没有「均」，即不用将根号里的东西乘以 。